GNSS Integer Ambiguity Resolution

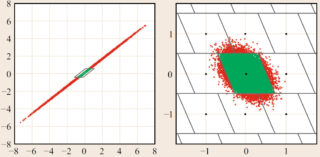
Several key issues need to be addressed in order to achieve the fullest exploitation of the opportunities created by future GNSSs. The highest possible accuracies can only be achieved if one is able to exploit the unique properties of the received carrier signals. These properties include the mm-level precision with which the carrier-phases can be tracked, the frequency-diversity of the carriers, and the knowledge that certain functions of the carriers are integer-valued. The process of exploiting these properties is known as integer ambiguity resolution (IAR).

IAR improves the precision of the estimated GNSS model parameters by at least two orders of magnitude. For positioning, successful IAR effectively transforms the estimated fractional carrier-phases into ultra-precise receiver-satellite ranges, thus making high-precision (cm to mm level) positioning possible. As a beneficial by-product, it also improves other GNSS model parameters, such as atmospheric parameters, and it enables reduction of GNSS parameter-estimation space, sometimes up to fifty percent, thus simplifying computations considerably and accelerating the time to position.

The success of IAR depends on the strength of the underlying GNSS model. The weaker the model, the more data needs to be accumulated before IAR can be successful and the longer it therefore takes before one can profit from the ultra-precise carrier signals. Clearly, the aim is to have short times-to-convergence, preferably zero, thereby enabling truly instantaneous GNSS positioning.

The theory that underpins ultra-precise GNSS parameter estimation is the theory of integer inference. Although a large part of the theory has been developed since the 1990s for GPS, the theory has a much wider range of applicability.